|
T
T | U | V |
W | X | Y | Z
table
(1) a list of values for two or more variables that shows the relationship between them; (2) any chart that displays data
tablespoon (T or tbs.)
a US customary measure, usually of food equal to 1/16 cup
tally
to count or record individual responses to a poll or questionnaire
tally system 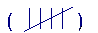
a method of counting and marking numbers in groups of five
When we tally large numbers of responses, we often make four vertical lines and then put a diagonal slash through them to mark the fifth response. Using the tally system makes it easier to count the total when we’re through.
tangent of an angle (tan  ) )
the trigonometric function that for an acute angle is the ratio between the length of the side opposite and the length of the adjacent side
tangent to a curve at a point
the straight line that just touches the curve at a particular point
A curve can have an infinite number of tangents, but it has one and only one tangent at any given point.
Tangents to curves are used in calculus.
teaspoon (t. or tsp.)
a US customary measure, usually of food or liquids equal to 1/3 tablespoon
terminating decimal
a decimal that has a final non-zero digit; when dividing a fraction to convert it to a decimal, the quotient that results when a remainder of zero occurs
terms of a variable expression
the parts of an expression that are separated by a plus or minus sign
A term might be something terribly simple, like a signed number (a constant term) or a signed variable standing alone. Variable terms can be much more complex; they can involve multiplication and division of the variable. For example,
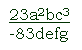
looks very complex, but since every number and variable there is being multiplied or divided, it counts only as one term.
tesselation
a pattern using one or more identical shapes which fit together without gaps to fill space; tiling
The above designs are examples of tesselation.
tetrahedron
a solid with four triangular faces; a triangular-based pyramid
three-dimensional figure
a figure that has length, width, and height; a figure that has both surface area and volume; a
solid figure
time zone
one of 24 regions of the earth, each 15° wide in longitude. All the people in each time zone use the same clock time.
As the earth rotates on its axis, the sun appears on the eastern horizon in the event we call sunrise. If we call a friend who lives 100 km west of us exactly at the moment that the sun peeks into view, they will tell us that they can see light outside, but that sunrise hasn’t happened there yet. The earth rotates at a constant speed, so people experience sunrise at different moments, depending on how far east they are.
For most of history, people in each town could set their clocks however they chose. Perhaps there was one big clock in the center of town, and people all set their watches and clocks by it. However, in the eighteenth and nineteenth century, advances in transportation (railroads), communication (telegraph), and technology (chronometer to read longitude at sea) led to a desire to “synchronize our watches,” to make it easier to set up train schedules and the like. In the late 1800s, people
decided to set up time zones. Greenwich, the area of London, England, that housed the Royal Observatory, was chosen as the 0° longitude, and the time there was called Greenwich Mean Time (GMT). The globe was divided into 24 zones, each of them 15° wide in longitude. When people in longitudes 0°-15°W were at noon GMT, people in longtidues 15°W-30°W would be at 11 am, people living
31°W-45°W would be at 10 am, and so on. These became the standard time zones.
Daylight Saving Time (called Summer Time in some countries) was a later innovation.
times sign (x)
the symbol (x) that shows multiplication
Multiplication can also be shown by placing a centered dot (·) between the numbers being multiplied [as in 4·3 = 12] or by writing the numbers next to one another, separated only by parentheses [as in 4(3)=12].
ton (most often abbreviated t.; also, T. or tn.)
a US customary unit of weight equal to 2000 pounds
topology
the branch of mathematics studying what happens to shapes when they are pulled or stretched; “rubber sheet geometry”
total
sum
transversal
a line intersecting two other lines at different points
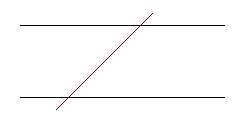
The red line in the above figure is a transversal. The two lines that a transversal do not have to be parallel, but if they are, there are many properties about the angles made. (See alternate exterior angles, alternate interior angles.)
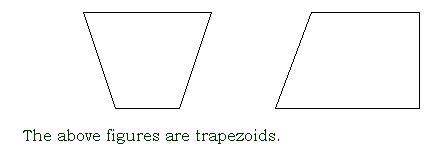
trapezoid
a quadrilateral with only one pair of parallel sides
tree diagram
a diagram used to show all possible combinations in order to solve a problem
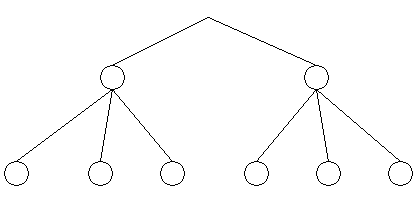
The above figure is an example of a tree diagram. This one could be used, for example, to figure out how many outfits (combinations) I could make from two pairs of slacks and three sweaters.
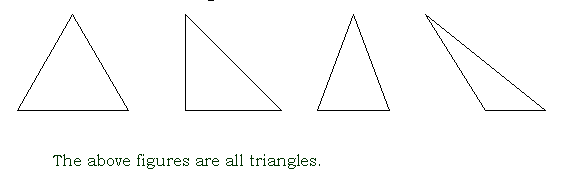
triangle
a three-sided closed figure
trigonometry
the branch of mathematics dealing with the ratios of sides of right triangles, which has numerous scientific and engineering applications
true proportion
a proportion in which the fractions are equal when written in lowest terms; a proportion in which the scale factor is an integer.
1:2::3:6 is a true proportion because I can multiply both members of the first ratio by 3 to get the corresponding members of the second ratio. 1:2::1½:3 is a proportion, but not a true proportion, because I multiply each member of the first ratio by 3/2 to get the corresponding member of the
second ratio. When you are asked to find the missing member of a proportion, if it’s not a true proportion, use cross-multiplying to work it out.
top
U
union ( ) )
the set that results from combining two sets
When I list the members of the union set, I list every member that is only in the first set and every member that is only in the second set, but if there are any members common to both original sets, I list them only once in my union set.
Formally stated: Given sets A and B, the set of all elements that are in set A or in set B or in both sets.
We use the symbol to show the union of sets. We write A to show the union of sets. We write A
 B; we say, “A union B”. B; we say, “A union B”.
For example, A = {1,2,3,4,5} and B = {1,3,5,7,9}. Then A  B = {1,2,3,4,5,7,9}.
B = {1,2,3,4,5,7,9}.
unit cost
the cost of one unit of a product
For example, if it cost $3.60 to bake 5 dozen cookies, each cookie cost six cents to make, so that’s the unit cost.
unit fraction
a fraction with a numerator of 1 and a nonzero integer as denominator
All unit fractions are in lowest terms.
unit of measurement
the word or words following the number part of a measurement telling what standard was used in the measuring process
Units of measurement for length include centimeter, meter, kilometer, inch, foot, yard, mile, etc. The unit of measurement for temperature is degree, but you should specify whether you used a
Fahrenheit or Celsius thermometer. Units of measurement for weight include milligram, gram, kilogram, ounce, pound, and ton.
unit price
the price for one of something; the total price for a bunch of identical things divided by the number of things in the bunch
Unit pricing is the key to comparative shopping. If type A of apple is priced 4 for $1 and type B is 15 for $3, which is the better deal? The unit price for type A is 25 cents ($1 ¸ 4), and but the unit price for type B is only 20 cents ($3 ¸ 15), so B is cheaper.
unit rate
a rate in which the number in the denominator is 1
unknown
same as variable
unlike fractions
fractions that have different denominators
You can multiply and divide unlike fractions, but before you try to add or subtract them, you must first convert them to equivalent like fractions.
top
V
variable
a quantity in an algebraic equation or expression that can change, that can take on different values in different circumstances; a symbol that represents numbers; a number associated with a set, any element of which may be used to replace the variable
We use letters of the alphabet to symbolize the variables of an equation. One exception is p, the Greek letter pi. That’s an alphabet letter, but in equations and formulas it’s a constant, the ratio of the circumference of a circle to its diameter, which never changes.
Equations and expressions are made up of variable terms (terms that mean a number, but the number can change from time to time) and constant terms (numbers that have one constant value).
variable expression
an expression that contains one or more variables
Variable expressions include x, 25x2 + 6, -a2b, etc.
variable term
a term composed of a numerical coefficient and a variable part
Remember that any variable standing by itself is really that variable multiplied by1. When you are combining like terms of an expression like 4a –a, that’s really 4a – 1a, which simplifies to 3a.
vector
a physical quantity that has both size (magnitude) and direction
Velocity (speed in a given direction) is a vector quantity.
Contrast this with scalar, a quantity (like time) that has no direction.
Venn diagram
a diagram that shows relationships among sets
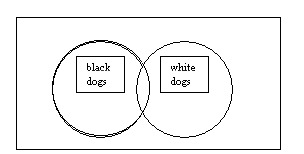
The above diagram is a rough Venn diagram. The rectangle represents the universe, the largest set we are talking about. Each circle represents one set in that universe. If the circles overlap, it means we expect there will be some elements in common between the two sets.
In our example, the universe is the universe of all dogs. Two sets in this universe are the set of all back dogs and the set of all white dogs. We overlap the sets to show that there are some dogs, like Dalmatians, which are black and white at the same time.
vertex (plural vertices)
a point where the two rays of an angle meet; (2) a point where two sides of a polygon meet; (3) a corner point of a polyhedron
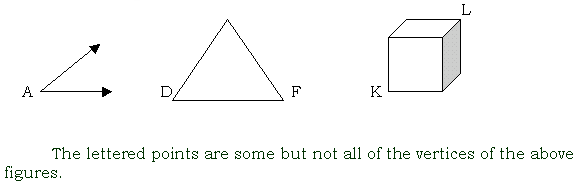
vertical
running straight up and down; running paralle to the way objects fall when dropped; running perpendicular to the horizon
vertical angles
two nonadjacent angles formed when two lines intersect
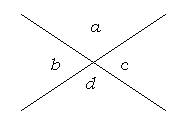
In the above figure,  a and a and
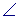 d are vertical angles and d are vertical angles and
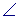 c and c and
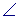 d are vertical angles. d are vertical angles.
Vertical angles are always equal.
volume
the amount of space that an object takes up or that an object can hold, expressed in cubic units
top
W
watt-hour
a unit of electrical energy in the metric system
weekly
every week
weight
a measure of how strongly the earth is pulling on an object
whole numbers
the set of natural numbers and the number zero, {0,1,2,3,…}
whole-number part
in decimal notation, that part of the number that appears before (to the left of) the decimal point
withdraw
take money out of an account
top
X
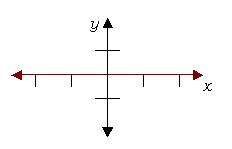
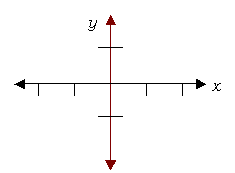
x-axis
the horizontal axis in a rectangular coordinate system
In the above coordinate system, the x-axis is marked in red.
x-coordinate
the first number of an ordered pair, which indicates how far the point is to the right or the left of the y-axis
x-intercept
a point at which a graph crosses the x-axis
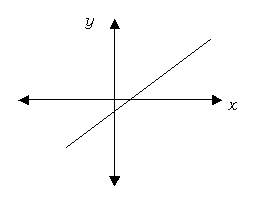
The line y = x – 1 crosses the x-axis at point (1,0), so the x-intercept for this equation is the point (1,0).
The value of y in every x-intercept is 0. To find the x value of the x-intercept, substitute 0 for y in your equation and solve for x.
Horizontal lines like y = -3 or y = ½ have no x-intercept.
top
Y
yard (yd.)
a US customary unit of length equal to 36 inches
y-axis
the vertical axis in a rectangular coordinate system
In the above coordinate system, the y-axis is shown in red.
y-coordinate
the second number of an ordered pair, which indicates how far the point is above or below the x-axis
yearly
every year
y-intercept
a point at which a graph crosses the y-axis
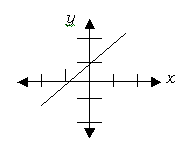
In the above rectangular coordinate system, the line y = x +1 is shown. This line crosses the y-axis at (0,1), so that point is called the y-intercept. If you have a line whose equation is written in the slope-intercept form y = ax + b, the y-intercept will be at point (0,b).
A graph of an equation can have more than one y-intercept. The graph of a line segment may or may not have a y-intercept. Any vertical line like x = -2½ or x = 14 will not have a y-intercept.
top
Z
zero product property
the property stating that if I multiply two numbers and get an answer of 0, then one of the numbers in my problem must be 0
Formally stated: For numbers a and b with a¹ b, if ab = 0, then either a = 0 or b = 0.
The zero product property comes in very handy when you’re trying to find the solutions to a quadratic equation. For example, if you have the equation x2 – 64 = 0, you can factor it to (x + 8)(x – 8) = 0. The two expressions inside the parentheses [(x + 8) and (x – 8)] are factors; according to this equation, when they’re multiplied together, they equal 0. Because of the zero product property, you know that either (x + 8) = 0 (meaning that x = - 8), or (x - 8) = 0 (meaning that x = 8). You now know that +8 and –8 are the two solutions to the equation x2 – 64 = 0.
zero power
To be consistent with the way that power is defined, any number taken to the zero power is 1.
Formally stated: For any number a, aº = 1.
Some mathematicians say, “a to the zeroth power” rather than “a to the zero power.”
Remember that any number taken to the first power equals the number itself. Formally stated: For any number a,
a¹ = a.
back to top
|


