S

salary 
pay based on a weekly, biweekly, monthly, or annual time schedule
People who receive a salary instead of hourly wages get paid the same amount each pay period, regardless of whether they worked 20 hours or 120 hours. People who receive a salary are usually higher paid than people who earn hourly wages, but the salaried workers do not receive time-and-a-half on weeks they work more than 40 hours.


sale price 
the reduced price


sample 
a small part of a larger group (which is called the population) which is used to study the larger group
Scientists take great pains to make sure that the sample they use in an experiment is truly representative of the population as a whole. If the sample is too small or is somehow biased, you cannot make valid generalizations based on it.


scalar
a real number that has no direction; a real number that can be used as a measurement, but not of any phenomenon (like velocity) that has direction as well as a number 
A scalar is the opposite of a vector, which has both a number and a direction.


scale 
(1) the ratio of distances on a model or map to real-world distances; (2) the distance between tick marks on the x- and y-axes of a coordinate grid; the labeling system used on coordinate system axes; (3) a tool for measuring weight


scale drawing 
a drawing that uses proportions to represent actual dimensions
Every scale drawing should include a key, an equation telling you how to convert from the measured lines on the drawing into the real dimensions of the object or place that the drawing is about. For example, if the key is 1 cm = 1 km, every line one centimeter long on the map will be one kilometer long in real life. 
When people design, say, a piece of furniture, they often start out sketching a rough idea of what the finished piece will be. A rough sketch is not “drawn to scale,” but is meant to convey a first impression of what the table would look like. Once the designers are satisfied with the style, they then take ruler in hand (or a design program on a computer) and make a scale drawing, because they need to know exact dimensions in order to calculate how much lumber is needed to build the table.
Architectural scale drawings are called blueprints, from the 20th century process that was used to produce them.


scale factor
the number you multiply the sides of a small figure by in order to enlarge it to a bigger but 
geometrically similar figure
For example, say I have two triangles. One has sides 3, 4, and 5 cm long; the second has sides 6, 8, and 10 cm long. If I take the first triangle and multiply each of its sides by 2, I get the second triangle. For these triangless, 2 is the scale factor, and they are similar figures.


scalene triangle 
a triangle that has no two sides of equal length, no two angles of equal measure


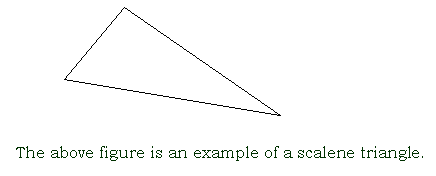
scientific notation 
a number expressed as the product of a number between 1 and 10 and a power of ten written in exponential form
Scientific notation is a very powerful shorthand way of writing very large or very small numbers. Scientists love it because numbers written that way can be multiplied easily and because they take up less room on paper.
For example, 6.0 x 1014 = 600,000,000,000,000 (six hundred thousand trillion). 4.18 x 10-5 = .0000418 (four hundred eighty ten millionths).


secant (sec )
the trigonometric function that for an acute angle is the ratio between the length of the side opposite and the length of the adjacent side


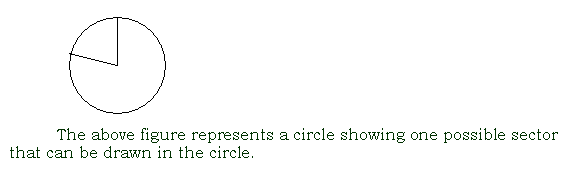
sector of a circle
a wedge-shaped piece of a circle formed by an arc of the circle plus the two radii of the circle that include the endpoints of the arc; the shape usually associated with pieces of a pie or round pizza


segment of a circle
the shape made by an arc of a circle and the chord that includes the endpoints of the arc

 
If the chord that segments the circle is a diameter, the two segments will be equal in size, and we call them semicircles.


selling price 
the price for which a business sells a product to a customer


semicircle
half of a circle; the shape made by an arc of the circle plus the diameter that includes the enpoints of the arc


set 
any collection of things
We usually group things, people, numbers, etc. together because they have something in common, but the members of a set are allowed not to have anything in common (except the fact that they belong to the set we are talking about).
We use the symbols { } to show a set, and inside those curly brackets we can either list the members of the set (with commas separating the members of the set) or we can describe the set in words. For example, we can write {1,3,5,…} or {odd numbers}; either way, we would read “the set of odd numbers”. We can also use a letter of the alphabet (usually a capital letter) to mean a set. 
We can write, A = {real numbers}.
Most of the time when we are dealing with sets, we’re interested in finding out questions like, Does this thing or number belong to the set? Do set A and set B have any members in common? What happens when I combine set A and set B? When we are collecting and organizing data, these questions occur all the time. If you understand set theory in mathematics, you’ll have no problem designing databases on computers: they are both based on what’s called Boolean logic.
We often use Venn diagrams to show the relationships among several sets.


side 
(1) one of the line segments that make up a polygon; (2) a ray of an angle



similar 
having the same shape but possibly a different size
Contrast this with congruent, which means having exactly the same shape and size.
If we have similar polygons, their corresponding angles will be equal, and their sides will be proportional.


simple interest 
interest compounded on the original amount
Contrast this with compound interest, in which every time the interest is calculated, it gets added to the original amount, so the next time the interest is calculated, it is calculated on a larger figure than the first time. Compound interest is the way most savings accounts and most loans are calculated.


simplest form 
having no common factors other than 1 between the numerator and the denominator; same as lowest terms
Why do tests almost always ask that a final answer involving fractions be written in 
simplest form (or lowest terms)? It’s because the smaller numbers that appear in a fraction written in simplest form are easier to use in real life. If I ask you to get me 128/256 of a cake, theoretically you are supposed to cut the cake into 256 pieces and then transfer 128 of them to my plate. If I say instead, “Give me half,” it’s the same amount, but you only have one cut to make and one piece to transfer to my plate. That’s much quicker. Fractions in simplest form are easier to imagine 
realistically.
Any fraction with 1 as the numerator and a positive or negative integer as the 
denominator is automatically in simplest form.
Any fraction that has prime numbers as the numerator and denominator with the smaller prime number as numerator is automatically in simplest form.
If I substitute the numerator and denominator of a fraction with its prime factors and I do not see any prime factors in common in the numerator and denominator, I know the fraction is in simplest form.


simplifying a variable expression 
combining like terms by adding their numerical coefficients


simultaneous equations
equations that share one or more solution
Simultaneous equations have at least one point where the x and y values work for both equations. If I graph two equations, the point or points where they intersect will be a solution to both equations.


sine (sin )
the trigonometric function that for an acute angle is the ratio between the length of the opposite side and the length of the hypotenuse


slant height 
the height of one of the lateral faces of a pyramid or the distance from the vertex of a cone to the circumference of the cone's base


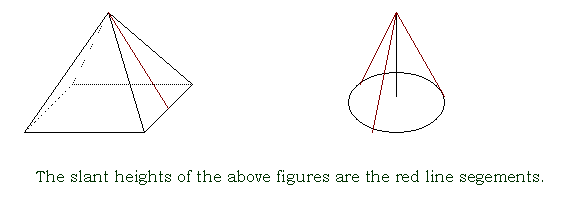
slope (m in the equation y = mx + b) 
the number that expresses the steepness of a line; ratio of vertical or horizontal change between any two points on the line; "rise over run"


solid 
an object in space


solution (of an equation or inequality) 
the value(s) of the variable(s) which make an equation or inequality is a true statement


solution set
the set of solutions which make an equation or inequality a true statement, used only when there are 
more than one solution


solving a proportion 
finding a number to replace the unknown so that the proportion is true


solving one-variable equations 
finding the value of the variable which makes the statement true


solving simultaneous equations 
finding values that make two or more equations true
There are algebraic ways to solve simultaneous equations, and there is a geometric way: plotting the two equations. Any point where the lines intersect on the graph a solution to both equations.


sorting 
arranging data in a specific order (e.g., alphabetic, numeric, date)


space
(1) the distance extending in all directions or in three dimensions, within which all things exist; (2) the distance, expanse, or area between, over, within, etc. things 
For meaning one, some scientists and mathematicians think of space as being infinite; others think of space as being finite, but so large that we can’t measure it.


speed 
distance traveled per unit of time


sphere 
a round three-dimensional figure in which each point on the surface is the same distance from the center; a set of points all at a fixed distance from a given point


spreadsheet 
a computer application program that creates tables and manipulates data in them; used mostly frequently for financial data, but can be used for any data that is mostly numbers and that you want to do math on


square 
a quadrilateral with four congruent sides and four right angles; a rectangle with four equal sides


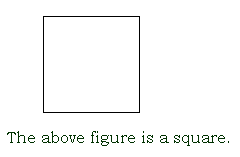
square centimeter (cm2)
a unit for measuring area equal to the area of a square with sides 1 cm long


square meter (m2)
a unit for measuring area equal to the area of a square whose sides are 1 m long


square number/perfect square 
the product of an integer multiplied by itself


square of a number/a number squared
the number multiplied by itself
Square numbers, also called perfect squares, must be integers, but you can square any number simply by multiplying it by itself.


square root 
one of two equal factors of a number


square unit 
any unit used to measure area


standard form 
a way of writing numbers using only the digits 0,1,2,…,9 plus commas, a decimal point, or a fraction bar as needed
Numbers written in standard form are numbers the way we are used to writing them, as integers, decimals, fractions and mixed numbers.


statistics 
the branch of mathematics concerned with data, or numerical information; facts of data of a numerical kind, gathered, sorted, and analyzed to present significant information about a given subject


story-telling from graphs 
reconstructing what must have happened in a situation by reading and correctly inferring from graphed data


straight angle 
a 180° angle; the angle made by a straight line


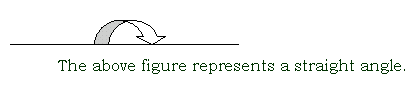
subset ()
a set each of whose elements is an element of another set
For example, if set B is the set of all women in the world and set A is all the women in math class, then set A is a subset of set B.
Formally stated: Set A is a subset of set B if every element in A is also in B.
We use the symbolto mean “is contained in”. If I write A B, I read aloud “set A is contained in set B”, which means A is a subset of B.
Every set is a subset of itself, and every set has the null set as a subset. All the other possible subsets are called proper subsets. 


substitute 
to replace a variable with another value, usually a number


subtraction 
the process of finding the difference between two numbers; finding out how many are left after taking some away from a group


subtraction facts
the whole number facts from 0 – 0 = 0 to 18 – 9 = 9, one hundred of them in all


subtrahend 
in subtraction, the number that is subtracted from another number (which is called the minuend); the smaller of the two numbers in a subtraction problem


sum 
in addition, the total of the numbers added


supplement 
one of two angles that have a sum of 180°. Each angle is the supplement of the other.


supplementary angles 
two adjacent angles with measures that add up to 180°


surface area 
the total area of the surface(s) of a solid figure


survey 
(1) to collect data; (2) to measure and map land


symbols
signs used in mathematics; “everything except the numbers” used in math class
Symbols include the letters we use to represent variables, comparison symbols, operation symbols, and grouping symbols.


symbolic form 
anything written or expressed through the use of symbols
symmetry the balance of a shape
Not every shape has symmetry.
Plane shapes can have line symmetry or rotational symmetry. Solid shapes can have plane symmetry, rotational symmetry, or point symmetry.





back to top