|
C
calculate
to determine a quantity, amount, etc., especially using higher mathematics
calculus
a special form of algebra good for studying constantly changing systems
Mathematicians disagree whether calculus was invented by Sir Isaac Newton or by
Gottfried Liebnitz. Either way, calculus gave mathematicians the tool they needed to study scientific
phenomena like gravity and accelerating movement.
calendar
a chart that shows months and days of a year
calorie
the basic unit of heat in the metric system; the amount of heat needed to raise the temperature of one
gram of water one degree centigrade
cancel (a fraction)
to divide the numerator and denominator of a fraction by the same number so as to reduce the
fraction to lowest terms
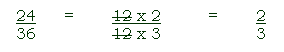
In the above example, we are allowed to cancel out the 12/12 because 12/12 = 1.
Multiplying or dividing a number by 1 does not change the the value of the number, so 24/36 and 2/3
have the same value, which means 24/36 = 2/3.
capacity
the amount (or volume) of space that a container can hold, measured in cubic units
cardinal number a counting number, whether written in standard form or using an English word (or a word from
another language)
Cardinal numbers answer the question, “How many?” They are the opposite of ordinal
numbers like first, second, third, and so on. Ordinal numbers tell what order a group of things is
arranged.
carry
in addition and multiplication, to regroup from a smaller place value to a larger place value
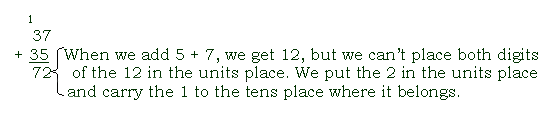
cell
the intersection of a column and row in a spreadsheet; the "box," identified by its column letter and
row number, which holds the data you type into it
Celsius (° C.)
the temperature scale of the metric system of measurement, in which the freezing point of water is 0
degrees and the boiling point of water is 100 degrees; also called centigrade
center of rotation
the one point which does not move when you do a rotation
Rotations are one of the tests we do to see if two figures are congruent. If the figures are
congruent, their size and shape must be exactly the same. If we could cut out one figure and place it
directly on top of the second figure, we could easily see if the two are exactly the same. However, if
the two figures are in a book, we can’t just go cutting it up. Instead, we imagine moving the first
figure on top of the second. We are allowed to slide it, to turn (or rotate) it, or to flip it in order to
see if it really is congruent. If we are rotating it, there will be one point on the paper that doesn’t
move. We rotate the figure around this point, which is called the center of rotation.
centi-
prefix for one hundredth
centigrade (° C.)
divided into 100 degrees; Celsius
centimeter (cm.)
a metric unit of measurement
1 centimeter = 0.01 meter
change
the difference between what you pay and what you owe; the difference between any two numbers or
between two values of a variable
In higher math, the idea of change is often symbolized by the capital Greek letter delta
(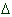 )
A
scientist talking about a change that happens over time might write )
A
scientist talking about a change that happens over time might write 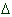 t or say “delta t”. t or say “delta t”.
charge
to add an amount to what you owe, especially when using a credit card
chart
a table of data
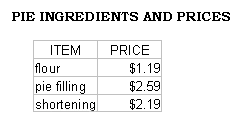
The above figure is a simple chart showing ingredients for a pie and corresponding prices.
chord
a line segment that connects two points on a circle

circle
a plane figure in which all points are the same distance from point O, which is called the center of the
circle
circle graph/pie chart
a graph in which pie-shaped parts of a circle represent data
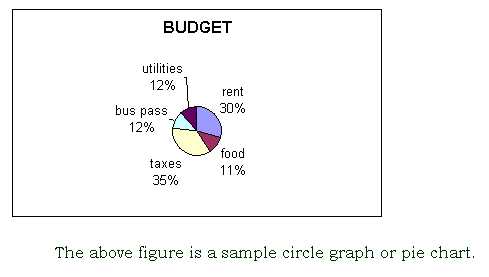
circumference (usually abbreviated as C in formulas)
the distance around a circle, equal to pi times the diameter
When we measure the distance around a figure that has straight lines for sides, we call it the
perimeter; only for circles do we call the distance around the figure the circumference.
clockwise
moving in the same direction that the hands do on an analog clock
closed set (under an operation)
describing the situation where we have a set of numbers, we choose an operation (addition,
subtraction, multiplication, or division), we do that operation on any two members of our set of
numbers, and we get an answer that is another member of that set
For example, let’s take the set of all positive integers (also called the set of counting
numbers). The set of positive integers is closed under addition and multiplication because if I add or
multiply two positive integers, I always get another positive integer. However, the set of positive
integers is not closed under division. When I divide 3 by 5, for example, I get the fraction 3/5, which
is not another member of the set of positive integers.
coefficient/numerical coefficient
the number multiplying the variable
In the equation y = 3x + 1, the number 3 is the numerical coefficient of x.
column
in a table, spreadsheet, or matrix, a vertical list of numbers or words that is read from top to bottom
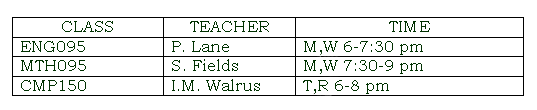
In the table above, there are three columns, one for CLASS, one for TEACHER, and one for
TIME. If you wanted to find one particular teacher, you would read down that column. Once you
found your teacher, you would read that row left to right to find the class and time.
commission
the part of the pay earned by a salesperson that is computed as a percent of the salesperson's sales
It’s frequent in the business world for a salesperson’s salary to be a combination of base pay plus a
commission. That means that the salesperson gets paid a small salary every week, but he or she gets
a much bigger paycheck on the weeks that they make lots of sales.
common factor
a number that is a factor of two or more numbers
For example, 4 is a factor of 8 (because 2 x 4 = 8). Four is also a factor of 20 (because 4 x 5 = 20).
So 4 is a common factor of 8 and 20.
common multiple
a number that is a multiple of two or more numbers
For example, 24 is a multiple of 8 (because 8 x 3 = 24). Twenty-four is also a multiple of 12
(because 12 x 2 = 24). So 24 is a common multiple of 8 and 12.
commutative property of addition, multiplication
The order in which numbers are added or multiplied does not change the sum or product.
Formally stated: For any numbers a and b, a + b = b + a and ab = ba.
compare
to decide whether a number is greater than, less than, or equal to another
comparison symbols
math symbols 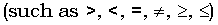 used to show how numbers compare
used to show how numbers compare
In math sentences, the comparison symbols act like verbs of being.
compatible numbers
pairs of numbers that are easy to work with. The pairs are based on basic multiplication and
division facts.
For example, 50 and 250 are compatible numbers because 250 divided by 5 = 50.
complement (as used in geometry)
one of two adjacent angles that have measures with a sum of 90°. Each angle is the complement of
the other.
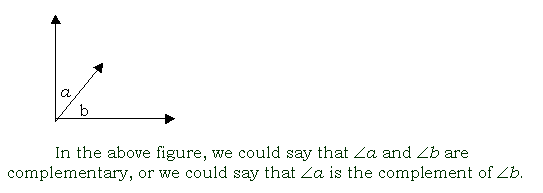
complement (as used in set theory)
The complement of set A (written sometimes as Ā sometimes as A¢) is the set of all elements that
are not in set A.
For example, think of all the students in a class. We could define set A as all the females in the class.
Then the complement of set A would be the set of all the males in the class.
complementary angles
two adjacent angles with measures that add up to 90°
complex fraction
a fraction in which the numerator or the denominator (or both) is a fraction or a mixed number

composite number
a natural number greater than 1 that has more than two factors; a whole number that is not a prime
number
For example, 24 is a composite number because 24 is the answer to several whole number
multiplication problems (1 x 24, 2 x 12, 3 x 8, and 4 x 6). On the other hand, 17 is a prime number
because it is the answer to only one whole number multiplication problem (1 x 17).
compound interest
interest compounded not only on the original amount but also on interest already earned
Almost all interest earned on savings accounts and interest charged on mortgages and other loans is
compound interest.
compute
find the number answer to a problem, usually by adding, subtracting, multiplying, dividing, or some
combination of those operations
concave polygon
a polygon in which at least one angle is greater than 180°

cone
a three-dimensional figure with a circular base and a vertex; a three-dimensional figure that has a
closed curve for a base and a surface that comes to a point
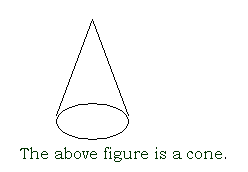
congruent 
having exactly the same size and shape
Contrast this definition with that of the word similar. Similar figures have exactly the same shape, but
they might be of different sizes.
conic sections
a group of curves that are formed by passing a plane through a cone
Examples of conic sections include curved lines, circles, parabolas, ellipses, and hyperbolas.
constant
a number that has a fixed value
A constant doesn’t have to be a terminating decimal number. Pi is a constant equal to 3.1416… and
2/3 is a constant equal to 0.6666… Pi and 2/3 are constants because their value never changes.
constant term
a term that has no variables; a "number" term
In the equation y = 4 x + 3, the 3 is the constant term. The 4 is a constant, but because it multiplies a
variable, we call it the coefficient.
continuous quantity
a quantity whose measurement can be any value
Quantities like weight, length, area, height, volume, temperature and speed are continuous quantities.
Quantities that are not continuous are called discrete quantities. The number of people in a closed
room is a discrete quantity because the answer can only be a whole number.
convergent
approaching a value
For example, if you look at unit fractions (fractions with a numerator of 1), you can build a set of
numbers {1/1, ½, 1/3, ¼, 1/5, …}. As the denominators get bigger, the fractions get smaller, but
they are always bigger than 0. We could say that the set of unit fractions is convergent or that the set
of unit fractions converges to 0.
conversion factors
ratios used to change units of measure
converting
changing from one unit of measurement to another
You divide to convert from a smaller to a larger unit of measurement and you multiply to convert
from a larger to a smaller unit of measurement.
convex polygon
a polygon in which any two interior points can be connected by a segment that is entirely within the
polygon; a polygon all of whose vertices point outward
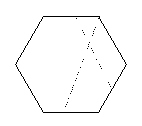
The above polygon is convex. All its vertices point outward and you can draw lines from one point
on the polygon to another without going outside the polygon.
coordinate/coordinate pair
the number associated with a point on a number line or one of two numbers that identify a point on a
coordinate plane
The coordinates for a point on a coordinate plane are an ordered pair of numbers. We
usually write the coordinates as (x,y), where x is the horizontal number line and y is the vertical
number line making up the coordinate system.
coordinate system/graph
two perpendicular number lines that intersect at zero
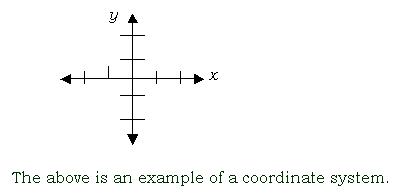
correlation
a relationship of one set of data values to another
Positive correlation means that as one value increases, the second value also increases. Negative
correlation means that as one value increases, the second value decreases.
correspondence
a relationship between elements of two sets
Famous types of correspondence include many to many correspondence, one to many
correspondence, many to one correspondence, and one to one correspondence.
corresponding angles
two angles that are on the same side of the transversal and are both acute angles or are both obtuse
angles
cosecant
(csc  ) )
the trigonometric function that for an acute angle is the ratio between the length of the hypotenuse
and the length of the opposite side
cosine
(cos  ) )
the trigonometric function that for an acute angle is the ratio between the length of the adjacent side
and the length of the hypotenuse

cost
the price that a business pays for a product; price a consumer pays for an item; the decrease in
assets associated with any expenditure
cotangent (cot
 ) )
the trigonometric function that for an acute angle is the ratio between the length of the opposite side
and the length of the adjacent side
counterclockwise

moving in the direction opposite the way the hands on an analog clock move
counting numbers
the numbers we use to count things; the set of natural numbers, {1,2,3,…}; the set of positive
integers
credit
to add an amount to what you already have
cross multiplying/cross product
a method used to solve proportions by multiplying the numerator of one ratio by the denominator of
the other
cube
a rectangular solid in which all six faces are squares and all its edges equal in length
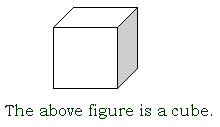
cubic centimeter (cc.)
a unit of capacity (volume) equal to 1 milliliter
cubic unit
the unit of measurement for volume or capacity
cup (c.)
a US customary measure of capacity equal to ½ pint
customary units
the units (inches, feet, yards, pounds, ounces, etc.) of the measurement system often used in the
United States
cylinder
a three-dimensional figure with two parallel congruent circular bases
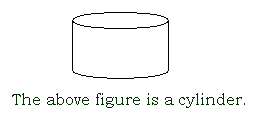
back to top
|