|
M
M | N |
O
map
scaled symbolic representation of a geographical area
mapping
a relation in which there is only one image for each object mapped
margin of error
the range of the most often obtained values around a predicted value
For example, 100 ±5% means 95-105. The ±5 % is the margin of error.
markup
the difference between selling price and cost
markup rate
the percent of a product's cost that is represented by the markup
mass
the amount of material in an object
On the surface of the earth, mass is very similar to weight. Weight measures the effect of gravity on mass. However, if you moved to the moon, your mass would stay the same, but the moon’s gravity is less than earth’s so your weight would drop.
mathematics
the group of sciences that use numbers and symbols to deal with quantities, magnitudes, and forms along with their relationships and attributes
Branches of mathematics include arithmetic, geometry, algebra, and calculus.
matrix
a rectangular array of numbers or letters
mean
the same as arithmetic mean or average: the sum of a list of related numbers divided by the number of items in the list
measurement
a number used to describe attributes of objects or natural phenomena (like size, capacity, or temperature) done by comparing the attribute of the object with a known standard (like a ruler or thermometer)
median
the middle term for a set of data that is arranged in order from least to greatest
If you have an odd number of numbers in your data set, the median will be the middle number itself. If you have an even number of numbers in your data set, you take the average of the two middle numbers. Thus, the median may be or may not be a number from your data set.
mediator
a perpendicular bisector; a line that cut a line segment exactly in half at right angles
There will be only one mediator for a line segment. It will act as the line of symmetry for the line segment.
member ( ) )
an element of a set
The symbol for “is a member of” is  . To write the sentence “Six is a member of the set of even numbers using set theory symbols, you would write 6 . To write the sentence “Six is a member of the set of even numbers using set theory symbols, you would write 6
 {2, 4, 6, …}. {2, 4, 6, …}.
meridians
the north-south imaginary lines on a globe; the longitude lines on a globe.
The prime meridian runs through Greenwich, England.
meter (m.)
the basic unit of length of the metric system
metric system
a system of measurement based on the decimal system, used by almost every country in the world except the United States
midpoint
a point that is halfway between two given points
midpoint formula
a formula for finding the halfway point between any two points on a coordinate system
Formally stated: If (a,b) and (c,d) are any two points, then M, the point midway between these two points, has coordinates given by M = ((a+c)/2, (b+d)/2).
mile (mi.)
a US customary unit of length equal to 5280 feet
mileage
number of miles traveled
Mileage is measured by an odometer for cars and by a pedometer for hikers.
miles per gallon (MPG)
the number of miles a vehicle can travel on one gallon of gas
milli-
prefix that indicates 0.001 units (thousandths)
milligram (mg.)
a unit of measurement equal to 0.001 gram
milliliter (ml.)
a unit of measurement equal to 0.001 liter
millimeter (mm.)
a unit of measurement equal to 0.001 meter (about the thickness of a dime)
minuend
in subtraction, the number from which another number (which is called the subtrahend) is subtracted; in an arithmetic subtraction problem, the larger of the two numbers in the problem
In addition and multiplication as it’s taught today, the two numbers making up your
problem have the same name: in addition they are called addends; in multiplication they are called multipliers or factors. That’s because addition and multiplication are commutative: it doesn’t matter what order you write your two numbers in an addition or multiplication problem. However, subtraction and division are not commutative, so it matters which number plays which role (subtrahend or minuend; divisor or dividend).
minus sign (-)
the symbol (-) that shows subtraction
mixed number
a number greater than 1 that has a whole number part and a fractional part; an improper fraction reduced to lowest terms
mode
the value that occurs most often in a given set of data
The mode will always be one of the numbers in your data set. Medians and averages do not have to be numbers from the original data set.
You may have more than one mode for a set of data. If every member of the data set is unique, then you do not have any mode for that data set.
monthly
every month
more than (>)
having a bigger number; greater than
The symbol for more than is >.
mortgage
the amount borrowed to buy real estate (land and buildings)
most
the largest or biggest
motif
a small shape or figure repeated in a tesselation or a pictogram
multiple
the product of a number and any whole number
Formally stated: If k is a counting number and n is a number, then
kn is a multiple of n.
multiplicand
an old-fashioned term for the first of the two numbers being multiplied in a multiplication problem
multiplication
the process of finding the product of two numbers
multiplication facts
the facts for which both factors are nine or less, one hundred facts in all
multiplication property of one
the property stating that any number times 1 is the number itself
Formally stated: For any number n, 1 times n = n.
This property makes 1 the identity element for multiplication.
multiplication property of zero
the property stating that any number times 0 is 0
Formally stated: For any number n, 0 times n = 0.
multiplicative inverse
the number which, when multiplied by another number, results in a product of 1. The two numbers are multiplicative inverses
of one another.
5 and 1/5 are multiplicative inverses because 5 x 1/5 = 1. The multiplicative inverse of a nonzero integer is 1 over that integer.
multiplier
now, one of the two numbers in a multiplication problem; the same as factor; formerly, the second of the two numbers in a multiplication problem (the number doing the multiplying)
multistep problem
a math problem that requires more than one operation to solve
top
N
natural numbers (positive integers)
the set of counting numbers, {1,2,3,…}
The set of natural numbers does not include 0.
necessary information
information needed to solve a problem
If you lack necessary information, you won’t be able to solve the problem. If you have
unnecessary information in addition to the necessary information, you’re going to have to weed out
the irrelevant numbers before doing your problem.
negative integers
integers to the left of 0 on the number line
negative numbers
numbers (both integers and the numbers between integers) that are to the left of 0 on a number line
When you write negative numbers, you must always place a minus sign (-) before the
number. If you do not see the minus sign, you assume the number is positive.
Only the number 0 is neither negative nor positive.
net
a 2-dimensional (plane) shape that you cut and fold to make a 3-dimensional (solid) figure

net pay
amount left to take home after deductions are subtracted from gross pay
nonagon
a polygon with nine sides and nine angles
number
a math answer to the question "how much?" or "how many?"
Number is the idea of "how many"; a numeral is the symbol you use to write that idea.
number line
a line used to represent the set of real numbers
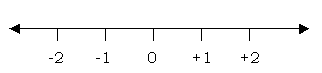
The above figure is a number line. You can use the number line to help you add and
subtract. You can use it to compare two numbers, because the number farther to the right on a
number line will always be greater than numbers to its left. You can also use a number line to graph
inequalities.
number sense
knowing what a number means and how to use it
number sentence
a mathematical sentence that gives the relationship between two expressions, which are composed of
numbers and operation signs
2 + 6 = 8; 4 > 2 + 1; and 3 < 6-1 are all number sentences. The comparison symbols
act as the main verb of each sentence.
number series
a set of numbers that progress according to a rule
numeral
the symbol used to write a number
Each numeral system uses different symbols. The Roman numeral system uses I, V, X,
L, C, D, and M in different combinations. The Arabic numeral system used today is a decimal-based
system: it uses ten basic symbols {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} in different combinations to make up
all numbers.
numerator
the part of a fraction that appears above the fraction bar; the top number of a fraction; the part of the
fraction telling how many parts out of the whole have been chosen
numerical term
in an equation or an expression, the term without a variable
In the equation y = 4x + 3, the 3 is the numerical term. The 4 is the numerical coefficient
of the x term.
top
O
obtuse angle
an angle with a measure between 90° and 180°

obtuse triangle
a triangle that has one obtuse angle
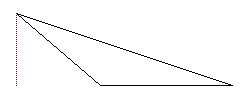
The above figure is an obtuse triangle with its altitude (or height) shown by the red dotted
line. The altitude is outside the figure for obtuse triangles.
An obtuse triangle can have only one obtuse angle because the sum of the angles in a
triangle = 180°, and if we had two obtuse angles, their sum would automatically be greater than
180°, leaving none left for the third angle.
octagon
a polygon with eight sides and eight angles
Stop signs on US roads are octagons.
octahedron
a solid shape with eight faces
The faces of a regular octahedron will all be equilateral triangles.
odd number
a whole number that is not a multiple of 2; a number that is one more than an even number
odometer
an instrument that measures distance traveled
operation
a way of combining elements of a set
The operations in arithmetic are addition, subtraction, multiplication, and division. The
operations in set theory are union and intersection.
You need to understand the properties of the various operations. Is the operation
closed? Does the operation have an identity element? Does every member of the set have an
inverse? Is the operation associative? Is the operation commutative? If two operations appear in the
same expression, is one distributive over the other one?
opposite sides
the sides of a quadrilateral that do not have a common endpoint
opposite vertices
the vertices of a quadrilateral that are not consecutive
opposites
numbers that are the same distance from zero on a number line but in different directions; additive
inverses
Additive inverses have the same absolute value, but different signs.
order of operations agreement
a set of rules that tells us how to simplify or solve equations and expressions by telling us the order in
which different mathematical operations are performed
The order of operations agreement says: (1) do whatever is inside parentheses or other
grouping symbols first; (2) do powers second; (3) do multiplcations and divisions from left to right
third; and (4) do additions and subtractions from left to right last.
For example, to solve (10 – 2) + 62 – (18-16)/2 + 6(4), first, do what’s in parentheses,
resulting in: 8 + 62 – 2/2 + 6(4). (Notice that you leave the last set of parentheses because they
show multiplication. There was nothing to “do” inside those parentheses.) Second, do the powers,
resulting in: 8 + 36 – 2/2 + 6(4). Third, do multiplication and division from left to right, resulting in: 8
+ 36 – 1 + 24. Finally, do addition and division from left to right, resulting in 67.
ordered pair/coordinate pair
a pair of number, with specified order, that can be used to designate a point on the coordinate plane
Ordered pairs are written in parentheses with a comma between the numbers, for
example: (6,10). The first number in the pair always represents how far left or right from 0 you are
on the horizontal x-axis. The second number in the ordered pair always represents how far up or
down from 0 you are on the vertical y- axis.
ordinal number
a number that indicates order, as in a series
Ordinal numbers tell us where a thing stands in line. Examples are first, second, third,
fourth, fifth, and so on. Ordinal numbers are the opposite of cardinal numbers, which are the
numbers we count with, the numbers that tell us the answer to the question, “How many?”If you add an “s” to any ordinal number greater than or equal to third(s), you have the
names for the denominators of fractions.
origin
on a number line, zero; in a coordinate plane, the point (0,0)
original price/regular price
the full price; the selling price before any discount is deducted
ounce (oz.)
a US customary unit of weight equal to 1/16 pound
outcome
a possible result of an action
output
for a function, the result after evaluating for given input; the y value that results for a given x
overtime
a higher hourly wage (usually 1½ times the regular hourly rate) earned by hourly workers when they
work more than 40 hours in a given week
US labor law requires employers either to pay “time and a half” for any hours over 40
worked in a given week, or to offer the employee compensatory time off – paid time off without that
is not counted against vacation or personal time. Some union contracts specify a higher overtime rate (double time or triple time) for employees who
work unpopular hours, like between midnight and 7 am on weekends.
back to top
|