abacus
a device used to count
An abacus often has a wooden frame with strings attached. Each string has a number of beads, and you count on it by moving beads to new positions. The abacus is traditionally used in Japan and China.


absolute value 
the distance of a number on the number line from zero
Because it is a measurement of length, distance is always positive. Absolute value is a distance, so the absolute value of a number is always positive. 


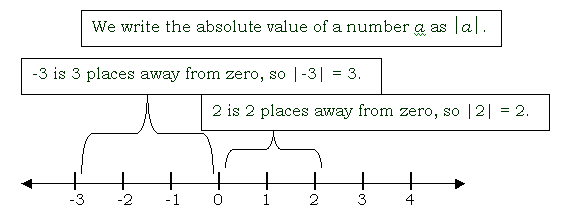
acceleration
the change in speed per unit of time


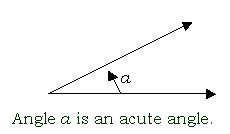
acute angle 
an angle with a measure between 0° and 90°


acute triangle 
a triangle that has three acute angles


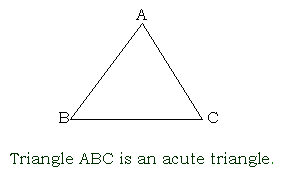
addend 
in addition, any one of the numbers added
The addends are the numbers that make up the addition problem. The sum or the total is the answer to the addition problem.


addition 
the process of finding the total or sum of two numbers; the arithmetic operation that combines amounts; the process of moving to the right on the number line
We use the plus sign (+) to show addition in a problem. 
An addition problem can be written either vertically or horizontally.


addition facts
the sums of each possible pair of addends from 0 + 0 to 9 + 9; one hundred of them in all


addition property of zero 
Adding zero to a number does not change the number. 
Stated formally: For any real number a, a + 0 = a and 0 + a = a.


additive inverse
the number which, when added to a given number, totals 0
For example, -3 and +3 are additive inverses of one another because –3 +3 = 0 and +3 – 3 = 0.


adjacent angles 
angles that have the same vertex, have a side in common, and do not overlap


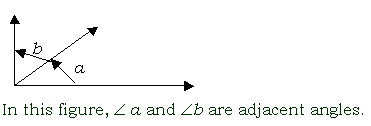
adjacent sides 
sides of a polygon that have a common endpoint


In rectangle ABCD, sides AC and AB are adjacent sides because they share common endpoint A.


algebra 
a mathematical system that generalizes arithmetic by using signed numbers and by letting letters or other symbols stand for numbers 
The word algebra comes from Arabic words meaning “the reunion of broken parts.” The more you work with algebra equations, the better you understand that meaning. As you combine like terms and do the other things you need to simplify an equation, you come to understand that an algebra equation is a number that has been broken up into many parts. As you go about solving for x, you reunite the parts.


algorithm 
a set of rules for performing a procedure; a special method to solve a certain kind of problem
For example, one algorithm for computing the area of a rectangle is to measure the length and width of the rectangle [using the same unit of measurement] and then to multiply the length times the width.


alphanumeric system
the system used in computer spreadsheets and on many maps in which the vertical coordinates are numbered and the horizontal coordinates are letters (or vice versa)
When you use an alphanumeric system to find a street on a city map, first you look up the name of the street in the index, and you find a code (for example, J2) next to the name. You use that code to locate the street on the map by finding column J, finding row 2, and looking in the section of the map where that column and row intersect.


alternate exterior angles 
two angles that are on opposite sides of the transversal and that lie outside the parallel lines


alternate interior angles 
two angles that are on opposite sides of the transversal and that lie between the parallel lines


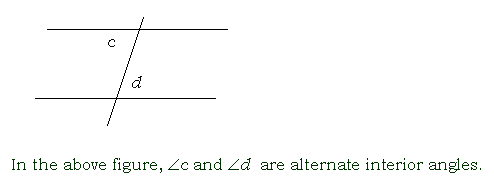
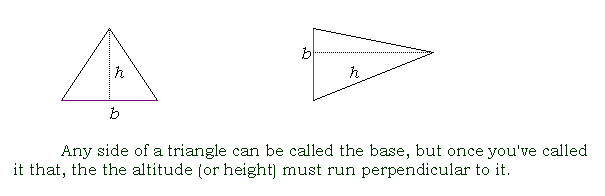
altitude of a triangle (usually abbreviated as h in formulas)
the line from a vertex of a triangle drawn perpendicular to the side opposite the vertex


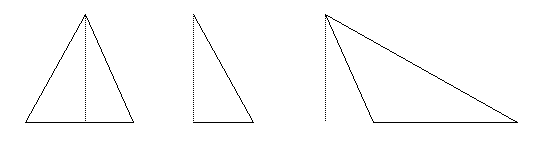
In the above three triangles, the altitude is marked by the dotted line. Notice that the altitude can lie inside an acute triangle or outside an obtuse triangle. In a right triangle, the altitude will be one of the legs.
With triangles, you are allowed to choose which side will act as the base. However, once you choose your base, you need to draw the altitude (or height) as a line perpendicular to your base ending at the vertex opposite the base.


altogether 
every one of something; in all
For example, Claire has six pennies in her left hand and four pennies in her right hand. If I ask, “How many pennies does she have altogether?” the altogether tells me to add to get the answer.


amount 
the sum or total of something; the quantity or value of something
Sum and total are words that also mean the answer to an addition problem; amount can be a more general word meaning how much of something. For example, I can say, “Mix the flour with a small amount of water.” Here I am leaving it up to you how much water is a “small” amount.


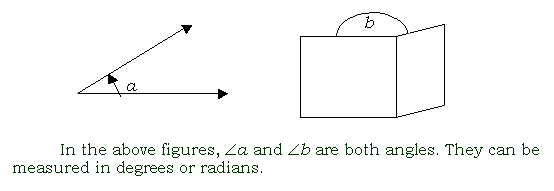
angle () 
the shape made by two rays meeting at a common point (called a vertex) or by two plane surfaces meeting along a line; the space between two such rays or plane surfaces


angle of depression
the angle measured downward from the horizontal to an object


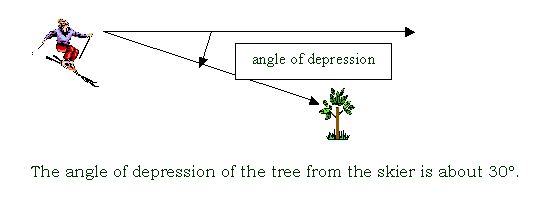
angle of elevation
the angle measured upward from the horizontal to an object



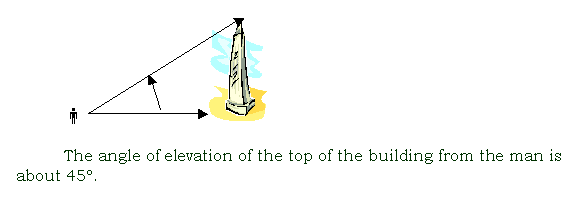
arc
a portion of a circle

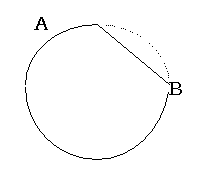
In the above freehand circle, arc AB is shown by the dotted line. The line segement AB is called a chord. If the chord happened to be a diameter of the circle, then arc AB would be a semicircle.

area (usually abbreviated as A in formulas)
the size of a surface, given in square units
You can compute the area of a plane (2-dimensional) figure or the area of a surface on a solid (3-dimensional) figure; however, when you refer to the area of all the surfaces on a solid, you call it surface area.


arithmetic 
the art or science of computing using positive real numbers and zero, specifically by adding, subtracting, multiplying and dividing

Arithmetic comes from a Greek word meaning “the art of counting.”
When you add, subtract, multiply, or divide, you are, in some way, counting. Addition by ones is plain counting. Subtraction by ones is counting backward. Multiplication by twos is really repeated addition of one plus one, so it’s counting, too – just a fancier form of counting.
The word arithmetic has two pronunciations. When it’s used as a noun to mean a branch of mathematics, it’s pronounced uh-RITH-met-tick. When it’s used as an adjective (as in the phrase arithmetic mean or arithmetic sequence), the accent moves. As an adjective, it’s pronounced AIR-rith-MET-ick.


arithmetic mean
the same thing as average or mean (See those terms for a more complete description.)
Mathematicians use the more precise term arithmetic mean because there is another kind of mean, a geometric mean, and mathematicians don’t want anyone to be confused about which one they used.


arithmetic sequence
a number sequence that is obtained by adding the same number to the number before it in the sequence
For example, the sequence {1, 4, 7, 10, …} is an arithmetic one because you get each term by adding 3 to the term before it.


associative property of addition/associative property of multiplication 
the idea that grouping does not affect the sum or product of three numbers. When I add three numbers or multiply three numbers, the order in which I do the addition or multiplication doesn’t matter.
Formally stated: For real numbers a, b, and c, (a + b) + c = a + (b + c) and (ab)c = a(bc). 


at 
for the price of
For example, “Ben bought three pens at $1.19 each.” 
The symbol @ is used for at, both in math problems and in Internet addresses.


attribute 
a characteristic that distinguishes an object from other objects
For example, the geometric shapes that we call quadrilaterals share the attribute of having four sides. Rectangles, rhombuses, squares, trapezoids and parallelograms all have this attribute, but a triangle (which has only three sides) does not have this attribute. Attributes are the qualities that allow us to group similar objects or numbers together and to decide when an object or number doesn’t fit in a group.


average 
the arithmetic mean of a group of numbers, computed by adding the list of numbers and then dividing by the number of items in the list; a common measure of central tendency
For example, to find the average of 2, 4, 6, and 24, first add them up. 2 + 4 + 6 + 24 = 36. Then count up the number of items on your list (4), and divide that into your total. (36 divided by 4 = 9). Note that the average does not have to be one of the numbers in your original list.


axes 
the plural of the word axis; in the rectangular coordinate system, the two number lines that intersect to form right angles



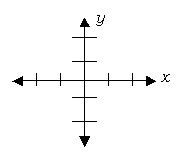
In the above rectangular coordinate system, the two axes are labeled x and y.

axiom
in geometry, an assumed statement that is applicable to the entire field of study



top

B

balancing a checkbook 
determining if the checking account balance is accurate
You balance a checkbook by comparing the monthly bank statement to the figures in your checkbook register and the receipts that you received from various transactions. Your ATM and other withdrawals and all the checks you wrote should balance all your deposits plus your initial balance.


bar graph 

a graph that displays data as parallel bars
Some people and spreadsheets programs distinguish a bar graph from a column graph by saying that a bar graph has horizontal bars, whereas a column graph has vertical bars. Others choose to call both bar graphs.


base 
the number that is raised to a power
In the expression 43, 4 is the base, the number we are raising to the third power (or cubing).


base of a triangle (usually abbreviated as b in formulas) 
the side to which the line segment for the height of the triangle is drawn



base ten number system 
also called the decimal number system; the number system we use in everyday life, which uses ten basic symbols {0,1,2,3,4,5,6,7,8, and 9} and makes up all other numbers using combinations of these ten basic symbols 


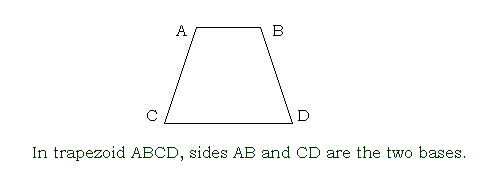
bases of a trapezoid (usually abbreviated as b in formulas) 
the two parallel sides of a trapezoid



basic percent equation 
"Percent times base equals amount"; also stated "Percent times the whole equals the part."


bearing
the angle measured clockwise from north to the object
Bearings are measured in degrees. You must always use three digits for a bearing. For example, you would write bearing 035°, not 35°.


benchmark 
a number that can be used to estimate the size of other numbers; a mark representing a known number, used as a reference point
For example, on some amusement park rides, only children over a certain height are allowed. The person running that ride might make a black line on the gate to the ride at the minimum allowable height. He uses the line as a benchmark to decide if a child is tall enough to go on his ride.


binary number system
a number system which uses only two digits (0 and 1) to make up all numbers


bisect 
to divide a line segment into two equal parts; to divide a shape into two congruent parts

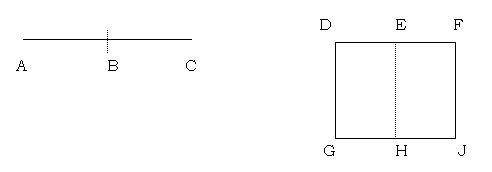
In the above figure (left), if line segment AB equals line segment BC, then the dotted line bisects line segment AC. If the above rectangle DEGH is congruent to rectangle EFHJ, then the dotted line segment EH bisects rectangle DFGJ.


borrow
in subtraction, to regroup from a larger place value to a smaller place value  

 

British thermal unit (BTU) 
a unit of heat; the quantity of heat needed to raise one pound of water one degree Fahrenheit


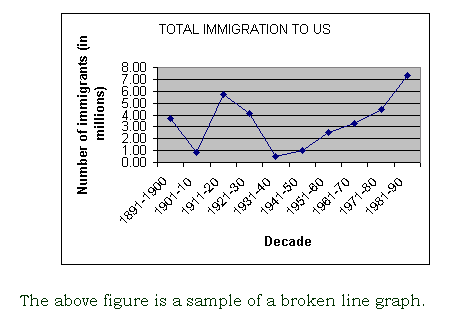
broken-line graph 
a graph that represents data by the position of the lines and shows trends and comparisons