|
D
D | E |
F
daily
every day
data
information, often numerical; facts, opinions, and numbers that are collected for study
Data is a Latin word. It is plural, so we write, “The data are conclusive,” not, “The data is conclusive.” If you want to refer to ALL the information you collected for study, you could call it the data set. If you want to refer to one tiny fact you collected, you could refer to it as a datum, but then the person you’re talking to might assume you know Latin.
Caveat emptor.
data analysis
a process for collecting, organizing, displaying and interpreting data
decagon
a polygon with ten straight sides and ten angles
decimal fraction
a fraction with denominator 10, 100, 1000, etc., when written in decimal notation
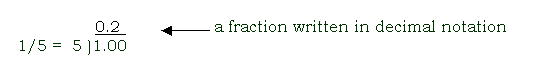
decimal notation
notation in which a number consists of a whole-number part, a decimal part, and a decimal point separating the two
decimal part
in decimal notation, the part of the number that follows the decimal point; the fractional part of the number
In the number 1941.618, we would say that .618 is the decimal part of the number.
decimal point
in decimal notation, the point that separates the whole number part from the decimal part
When you read a decimal number aloud, you can say “point” when you get to the
decimal point. You can also say “and” for the decimal point – if you say the decimal part of the number as a fraction ending –ths. For example, you can read a temperature 98.6° as “ninety-eight point six degrees” or as “ninety-eight and six tenths degrees.”
decrease
to make a number smaller
deduction
an amount (for example, state and federal taxes, Social Security) subtracted from earnings
The original amount you earn in each paycheck is your gross earnings. The amount you actually take home is your net earnings. Deductions are the difference between your gross and net pay.
degree (°)
unit used to measure angles; unit used to measure temperature
The symbol for degree is °. You write a small superscripted circle after the number. For example, the boiling point of water in the Celsius system of measuring temperature is 100°.
denominator
the part of a fraction that appears below the fraction bar, representing the total number of pieces into which one whole thing has been divided

The fraction 5/6 means that I took something and divided it into six equal pieces and used 5 of them. I used 5/6 of the thing I started out with.
density
the ratio of the mass of a substance to its volume
dependent variable
one of the two variables in a relationship, whose value depends on or is determined by the other (independent) variable
deposit
to add money to something such as a savings or checking account; the amount of money added to a savings or checking account
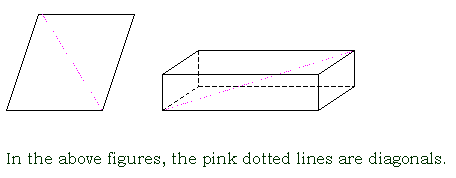
diagonal
a segment that joins two nonconsecutive vertices of a polygon or a polyhedron
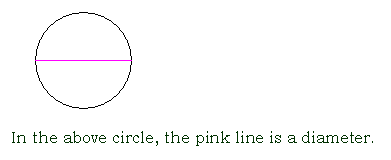
diameter of a circle (usually abbreviated d in formulas)
a line segment that passes through the center of a circle and has endpoints on the circumference of the circle; the longest chord that can be drawn inside a circle
diameter of a sphere
a line segment with endpoints on the sphere and going through the center
difference
in subtraction, the result of subtracting two numbers; the answer to a subtraction problem
differential equation
mathematical equation expressing the rates of change of quantities
digit
a symbol for a number {0,1,2,3,4,5,6,7,8,9}
Numbers from 0-9 are called one-digit numbers; from 10-99, two-digit numbers; from 100-999, three-digit numbers, and so on.
digital
a measuring system that uses whole numbers and decimals to show values
digital scale
a scale that shows weight as a whole number and a decimal
digital thermometer
a thermometer that displays temperature as a whole number and a decimal
dimensions (linear dimensions)
measurements (like height, length, width, or radius) associated with parts of a geometric figure
discount
the difference between the regular price and the sale price
discount rate
the percent of a product's regular price that is represented by the discount
discrete quantity
a quantity that has an exact answer to the question, “How many?”
For example, the number of people inside a room would be a discrete quantity because the answer to the question will be a counting number. We might have 10 or 1,124 people, but we wouldn’t have 15 ¾. Only natural numbers are allowed as possible answers. Similarly, if I ask how much money is in the cash register, the answer will be a discrete quantity because however much money there is, we can state it exactly in dollars and cents. We would never have an answer involing
fractions of a penny.
disjoint
able to be separated into categories that do not overlap
disjoint sets
two sets that have an intersection that is empty
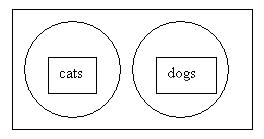
Let’s say that the above Venn diagram represents the universe of animals. Two of the sets in this universe would be the set of all dogs and the set of all cats. These two sets do not overlap – there are no dogs that are also cats. So the set of all dogs and the set of all cats are disjoint sets.
distance
a gap, space, or interval between two points, lines, objects, etc
distance formula
(1) the rule for calculating the distance traveled: Distance equals rate times time. (2) the rule for calculating the distance between two points on a coordinate system
Formally stated, d = rt, where d = distance, r = rate, and t = time. The formula for finding the distance between two points X(a,b) and Y(c,d,) on a coordinate system is
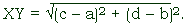
distributive property of multiplication over addition/subtraction
the rule that explains how to deal with or get rid of parentheses in some algebraic expressions if I am multiplying a number by the sum or difference of two numbers.
Formally stated: For numbers a, b, and x, x(a + b) = ax + bx and
x(a – b) = ax - bx.
Sets have a distributive property, too. For sets, the intersection operation is distributive over the union operation. Formally stated:
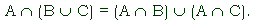
dividend
in division, the number into which the divisor is divided to yield the quotient; in finance, the amount of money that your money earns by being put to use in a certain way
division
the process of finding the quotient of two numbers
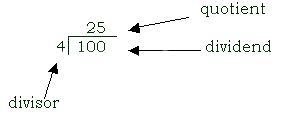
division facts
division problems in which the divisor and quotient are whole numbers not larger than 9, ninety of them in all
division symbols
symbols (/, ¸) used to show division
divisor
in division, the number that is divided into the dividend to yield the quotient; the number being divided by
dodecagon
a polygon with twelve straight lines as sides and twelve angles
dodecahedron
a 3-dimensional solid figure with twelve faces
If the dodecahedron is regular, the twelve faces will be pentagons.
domain of a function
the set of numbers you are allowed to use for your independent variable
Contrast this with range of a function, which is the set of numbers that result for your dependent variable.
Formally stated, the domain is the set of numbers mapped by the function.
duodecimal
a number written in base twelve
top
E each (@)
one person or thing; apiece
edge
in a polyhedron, the line of intersection of two faces
element of a set
one of the things or numbers in a set; a member of a set
empty set ({ } or f)
a set that has no members
An empty set is symbolized by curly brackets with nothing between them, as in { }, or
by f. For example, if set A = {all even numbers} and set B = {all odd numbers}, then A Ç B = { }
or A Ç B = f, because there is no number that is both even and odd.
energy
the ability to do work
English system of measurement
the system of measurement most commonly used in the United States (but no longer in England,
which now uses the metric system, like most of the rest of the world!)
equal sign (=)
symbol (=) showing that what appears to the left has the same value as what appears to the right of
the symbol
equally
where all have the same amount
equally likely outcomes
outcomes or events that have the same chance of happening
For example, if you toss a coin, there is only one “heads” and only one “tails.” Ordinarily
a coin tossed in the air will fall so that only “heads” OR “tails” will show. We say that the probability
of getting a “heads” and the probability of getting a “tails” are equally likely outcomes.
equation
a sentence stating that the value before and after an equal sign are equal; a rule containing variables
that represent a mathematical relationship
equiangular
figures in which all angles are congruent, having the same measure
equilateral triangle
a triangle with all sides of equal length
Every equilateral triangle has equal angles as well – three 60° angles.
equivalent expressions
two expressions that produce the same value
equivalent fractions
two or more fractions that represent the same number
If two fractions are equivalent, you will always be able to use cancellation to show that
they are equal.
estimate
to find the approximate value
evaluate
to find the value of an expression
If you are asked to evaluate an expression, the expression will have one or more
variables in it, and you will be given numbers for what each of those variables is worth. You
substitute the numbers for their matching letters in the expression, and then do the arithmetic to arrive
at an answer.
For example, to evaluate 3a + 2b, where a = 2 and b = 4, you look at your expression
and substitute a 2 wherever you see an a and you substitute a 4 wherever you see a b. In the
example, this substitution results in the expression 3(2) + 2(4). Then you do the arithmetic: 3(2) = 6,
2(4) = 8, so 3(2) + 2(4) = 6 + 8 = 14. The value of the expression 3a + 2b is 14 when a = 2 and b
= 4.
even number
a multiple of 2; in some countries, a “paired number” evenly where all have the same amount
evenly divisible by
a multiple of
event
a set of outcomes
exchange rate
rate in a formula, used to convert money from one country's currency to another's
Exchange rates between two currencies can change daily.
exponent
a raised number used to indicate the repeated multiplication of a number; a notation in which a
non-zero whole number is used to indicate the number of times that the base number is used as a
factor
exponential notation
the expression of a number to some power, indicated by an exponent
expression
a collection of variables, numbers and operation symbols (but no equal sign) that expresses a
mathematical relationship among the numbers and variables
For example, 4x + 3 is an expression.
extended form
a way of writing a number as an addition problem in which each addend in the problem represents
the place value of a digit in the original number
For example, the number 1,023,824 can be written in extended form as 1,000,000 + 20,000 +
3,000 + 800 + 20 +4.
top
F faces
the flat surfaces (polygons) of polyhedral solids
Polyhedrons are named according to how many faces they have. A cube has six faces; a
dodecahedron has twelve.
factor
a number that divides into another number and leaves a remainder of zero; in multiplication problems,
one of the two numbers being multiplied
Fahrenheit (°F.)
the temperature scale of the English system of measurement, in which water at sea level freezes at
32° and boils at 212°
fewer than
having a smaller number; less than
Fibonacci sequence
a sequence of numbers in which every number after the second number is equal to the sum of the
two preceding numbers
figure
a picture or chart or graphic representation of a problem
finite set
a set with a definite number of members
A finite set can be very, very large, but at some point it must stop: there must be a
definite number of elements.
fluid ounce (fl. oz.)
a US customary measure of capacity equal to1/8 cup
foot (ft.)
a US customary unit of length equal to 12 inches or equal to 1/3 yard
for
at the price of
formula
a way of expressing a rule using algebraic symbols and operations
Often a formula expresses a geometric or scientific truth. For example, the formula for
the area of a triangle is A = ½ bh, where b is the base of the triangle and h is its height.
fraction
notation used to represent the number of equal parts of a whole
fraction bar
bar that separates the numerator of a fraction from the denominator
friendly numbers
approximated numbers that are easy to work with
frequency
the number of times something (an event or outcome) occurs
For example, let’s say you’re a parent organizing a barbecue for the neighborhood kids.
You find out from the kids that 15 want chicken, 12 want burgers, and 8 want tofu hot dogs. Those
three numbers are frequencies.

frequency diagram
a bar graph showing frequency as the height of the bars
The above is a frequency diagram of the outcomes from asking 35 children what meal
they wanted for a neighborhood barbeque.
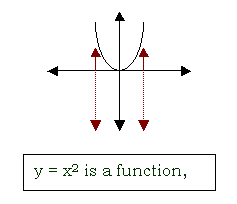
function
a special kind of relation in which each value given to the independent variable results in one and only
one answer for the dependent variable
There are many ways to state the idea of a function formally: Y is a function of x [written
y = f(x)] if and only if for every value of x, there is one and only one value for y. Or we could say
that y is a function of x if each object is mapped onto only one image.
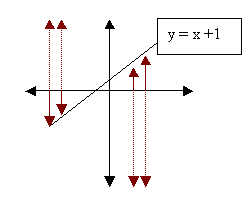
If you graph equations, you can inspect your graph to see if the equation is a function or
not. All linear equations except those resulting in a vertical line are functions. However, only some
conic sections are functions. To inspect a graph to see if the equation is a function, mentally walk
along the x-axis and keep looking left and right. If you see only point of the graph (meaning there’s
only one allowable value of y for that particular x), then you have a function. If there are two or more
y values for that point on the x-axis, you do not have a function.
 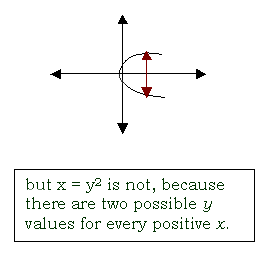
function keys
the keys on a calculator that indicate addition, subtraction, multiplication and division
fundamental theorem of arithmetic
the theorem stating that, except for the order of the factors, a whole number can be factored into
prime factors in only one way
back to top
|


