|
R
radicand
the quantity inside a root symbol; the number you are taking the square root of, or the cube root of, or the nth root of
radius of a circle (plural radii)
the distance from the center to any point on a circle; a line segment with one endpoint at the center of a circle and the other endpoint on the circumference
radius of a sphere
a line segment going from the center to any point on the sphere
raise
an increase in wages
range
(1) the difference between the greatest value and the least value for a given set of data; (2) for a function, the image set, the set of numbers that are values of the dependent variable
rate
a ratio that compares the measurements of two different attributes
For example, speed = distance/time.
ratio
a comparison of two numbers; the fraction formed when two quantities are compared by division
We can write ratios as fractions, like 2/3, or we can use a colon between the numbers, as in 2:3. If we use the colon notation, we read the expression “two is to three.”
ray
a straight path of points that start from one end point and extend indefinitely in one direction
We symbolize a ray by an arrow pointing in the direction in which the ray goes on
forever.
real numbers
the union of the sets of rational (terminating decimals) and irrational numbers
(nonterminating decimals); the numbers on a number line
reciprocal
the multiplicative inverse of a number
Formally stated: Every nonzero number a/b has a reciprocal, the number b/a.
For typical fractions, the reciprocal is the original fraction with its numerator and denominator switched. For example, the reciprocal of 3/8 is 8/3.
Zero has no reciprocal.
Since every whole number can be written as a fraction over 1, the reciprocal of a whole number is 1 over the whole number. For example, the reciprocal of 10 is 1/10.
rectangle
a quadrilateral with four right angles and opposite sides that are congruent
Parallelograms are a subset of the set of quadrilaterals. Rectangles are a subset of
parallelograms, and squares are a subset of rectangles. Each time we require more attributes of the figure: quadrilaterals need only have four sides; parallelograms need two sets of parallel lines as the four sides; rectangles require the two sets of parallel lines as sides plus four right angles; and squares require all of the above plus that the four sides be equal.
rectangular coordinate system
two perpendicular number lines intersecting at their zero points, producing a plane in which each point can be identified by an ordered pair; the same as coordinate system
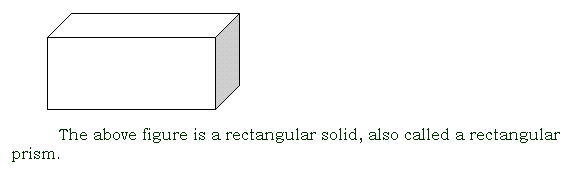
rectangular solid
a three-dimensional figure in which all lines meet at right angles; a prism with a rectangle as the shape that repeats itself along the length of the prism
reduce
to make a number smaller
reflection
a kind of transformation that makes the new figure a mirror image of the original figure
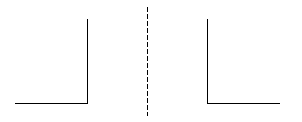
The above figure on the right shows a reflection of the figure on the left. The dotted line represents the line of symmetry, the plane where the mirror would sit in order to produce this kind of transformation.
reflex angle
an angle that is greater than 180° but less than 360°
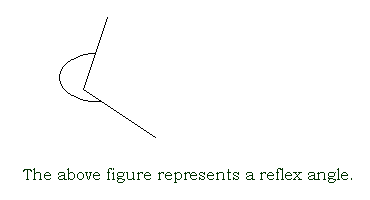
regroup
to borrow an amount from a larger place value in subtraction or to carry an amount to a larger place value in addition or multiplication
regular polygon
a polygon in which all sides are congruent (equal in length) and all angles have the same measure
The only regular triangle is the equilateral triangle. All triangles have 180° as the sum of their angles, so each equal angle of the equilateral triangle is 60°.
The only regular quadrilateral is the square. All quadrilaterals have 360° as the sum of their angles, so each of the four equal angles in a square is 90°.
Polygons with more than four sides also have 360° as the sum of their angles, so if you have a regular pentagon, hexagon, etc., you divide the number of angles into 360° to find the measure of each angle for these shapes.
relation/relationship
an association between two or more variables
Functions are a special type of relation, one in which each value of the independent
variable results in one and only one value for the dependent variable. A relation might have more than one.
remainder (R)
in division, the quantity left over when it is not possible to separate objects of numbers into a whole number of even groups
repeating decimal
the decimal that results from a division that does not ever come out evenly; a decimal containing one or more digits that repeat infinitely
When writing a repeating decimal, it’s common to draw a line over the digit or digits that repeat. For example:
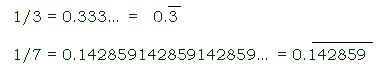
An alternative to drawing a line over the repeating digits is to place a dot over them, but this notation is infrequently used.
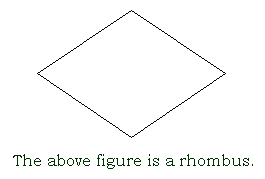
rhombus
a quadrilateral with four congruent sides and opposite sides that are parallel
A rhombus is a special kind of parallelogram, one that has all sides equal in length. If the rhombus happens to have 90° angles, it’s called a square.
right angle
an angle with a measure of 90°
We use a tiny square at the vertex to show a right angle.
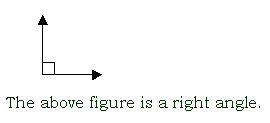
right angle property
If AC is a diameter of a circle and B is any point on the circumference of the circle other than A or C, then angle ABC is always a right triangle.
right triangle
a triangle with one right angle
right triangle 30-60-90
a special right triangle in which the length of the leg opposite the 30 degree angle is one-half the length of the hypotenuse
right triangle 90-45-45
a special right triangle in which the sides opposite the 45 degree angles are equal
rise
the vertical change between two points
For a line plotted onto a coordinate system, the rise is the change in the y-coordinates.
The slope of the line is rise/run, the change in y-coordinates over the change in the x-coordinates
root
the base that corresponds to a given power
root index
the number used to indicate what root to find
We use the radical sign (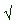 ) to show a root. If there is no number tucked into the radical sign, the root is automatically a square root. To show a cube root or higher root, we place a small superscripted number (the root index) inside the radical sign. For example, to show the cube root of 27, we write:
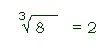
rotation
a transformation that rotates a shape a certain number of degrees about a point
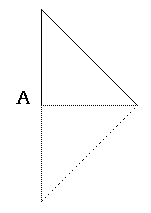
The dotted line figure shows the right triangle after it has been rotated 180° about point A. Point A, the center of rotation, is the one point of the figure that is invariant, meaning that it’s in the same place before and after the transformation.
rounding
using an approximate value (one that is close to an exact number but has more 0’s)
We round a number to a certain place value.
Normally, when we round, all the digits to the left of the desired place value will remain the same, and all the digits to the right of the desire place value will be replaced by 0’s. The only choice we have is to keep the desired place value the way it is (“to round down”) or to add 1 to that desired place value (“to round up).
We choose whether to round down or up by testing the digit to the right of the desired place value. If that digit is 5 or above, we round up. If that digit is 4 or below, we round down.
For example, to round 1,645,728 to the nearest thousand, we first find the thousands place value in the number (the digit 5).
The digits to the left (164) will remain, and the digits to the right (728) will be replaced by 0’s.
Our only choice is whether the 5 thousand will remain 5 thousand or whether we will add 1 to make it 6 thousand. To decide that, we look to the right of the 5. The digit 7 appears there. 7 is >5, so we round up.
So, the number 1,645,728 rounded to the nearest thousand becomes 1,646,000.
If the place value we are rounding to has a 9 in the original number and after we test, we decide to round it up, that 9 becomes a 10. Thus, the number 958 rounded to the nearest hundred becomes 1,000.
route on a map
a marking of the shortest way between two points on a map
row
a horizontal list of numbers or words that is read from left to right across a table
rule
a summary of a predictable relationship that tells us how to find the value of a variable
ruler
tool used to measure lengths
run
the horizontal change between two points
When an equation is graphed onto a coordinate system, the run is the change in the x-coordinates. The slope of the line = rise/run.
back to top
|
